Ogib-
Fresnelova
teorija
 Sva valna gibanja
pracena su pojavom ogiba, te se ona jednostavno moze uociti i u svakodnevnom
zivotu. Naime, primijeceno je da se valovi pri nailasku na prepreku o nju
‘povijaju’, tako da u podrucju gdje ne bi trebalo ocekivati valno gibanje ono
ipak postoji. To rezultira time da u podrucju iza prepreke, u kojem bi i bez
prepreke postojao val, zbog njenog prisustva val nije konstantnog iztenziteta,
vec ima minimume i maksimume, dok u podrucju gdje val nebi trebao postojati on
ipak postoji, i slabi sve vecim ulaskom u ‘sjenu’. Zbog ovog se pojava i naziva
difrakcija, sto prevedeno s latinskog korijena znaci ”razloziti na dijelove”.
Pojava se ocituje kod mehanickih valova, valova zvuka, radio-valova, valova
svijetlosti i drugih. Tako se, na primjer, morski valovi koji nailaze na
lukobran oko njega povijaju, te je iza njega more takoder valovito. Ukoliko se
koristi obicajen nacin prikaza svih valnih gibanja pomocu valnih fronti tj.
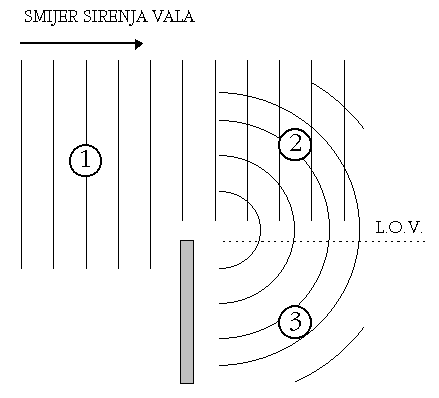
krivulja s jednakom fazom, to izgleda kao na Slici 2.1. Lako je uociti
elementarne cinjenice: valna duljina valova iza prepreke jednaka je valnoj
duljini valova ispred prepreke, a ogib je intenzivniji sto je frekvencija niza.
U cjelokupnom prostoru mozemo razlikovati tri podprostora: 1-ispred
prepreke, te 2- i 3-iza prepreke. U podrucju 1 postoji
uglavnom samo upadni val, u podrucju 2 upadni i difraktirani, dok
‘ispod’ linije opticke vidljivosti (LOV) postoji samo difraktirani
val. Ovo je jako pojednostavljen prikaz, ali dostatan za razumijevanje
fizikalnih osnova pojave ogiba. On je takoder posebno interesantan u optici
(opticka resetka, Newtonovi prstenovi) gdje sluzi kao dokaz i o valnoj prirodi
svijetlosti kao elektromagnetskog vala ekstremno visoke frekvencije.
Sva valna gibanja
pracena su pojavom ogiba, te se ona jednostavno moze uociti i u svakodnevnom
zivotu. Naime, primijeceno je da se valovi pri nailasku na prepreku o nju
‘povijaju’, tako da u podrucju gdje ne bi trebalo ocekivati valno gibanje ono
ipak postoji. To rezultira time da u podrucju iza prepreke, u kojem bi i bez
prepreke postojao val, zbog njenog prisustva val nije konstantnog iztenziteta,
vec ima minimume i maksimume, dok u podrucju gdje val nebi trebao postojati on
ipak postoji, i slabi sve vecim ulaskom u ‘sjenu’. Zbog ovog se pojava i naziva
difrakcija, sto prevedeno s latinskog korijena znaci ”razloziti na dijelove”.
Pojava se ocituje kod mehanickih valova, valova zvuka, radio-valova, valova
svijetlosti i drugih. Tako se, na primjer, morski valovi koji nailaze na
lukobran oko njega povijaju, te je iza njega more takoder valovito. Ukoliko se
koristi obicajen nacin prikaza svih valnih gibanja pomocu valnih fronti tj.
krivulja s jednakom fazom, to izgleda kao na Slici 2.1. Lako je uociti
elementarne cinjenice: valna duljina valova iza prepreke jednaka je valnoj
duljini valova ispred prepreke, a ogib je intenzivniji sto je frekvencija niza.
U cjelokupnom prostoru mozemo razlikovati tri podprostora: 1-ispred
prepreke, te 2- i 3-iza prepreke. U podrucju 1 postoji
uglavnom samo upadni val, u podrucju 2 upadni i difraktirani, dok
‘ispod’ linije opticke vidljivosti (LOV) postoji samo difraktirani
val. Ovo je jako pojednostavljen prikaz, ali dostatan za razumijevanje
fizikalnih osnova pojave ogiba. On je takoder posebno interesantan u optici
(opticka resetka, Newtonovi prstenovi) gdje sluzi kao dokaz i o valnoj prirodi
svijetlosti kao elektromagnetskog vala ekstremno visoke frekvencije.

Slika 2.2 Ogib svjetlosti na otvoru
Tako, na primjer, ako zrake svjetlosti naidu na prepreku sa otvorom a-b, na zastoru iza prepreke ostaje osvjetljeno podrucje A-B, pri cemu je opticka ‘slika’ otvora priblizno jednaka geometrijskoj. Medutim, ako je otvor reda velicine valne duljine svjetlosti osvjetljeni dio na zastoru bit ce i veci (C-D). Pojava se objasnjava ogibom valova svijetlosti. Pri ovome se javlja i pojava osvijetljenih i zatamnjenih prstenova unutar podrucja A-B zbog interferencije valova koja nastaje na ovakvoj slozenoj difrakcijskoj strukturi.
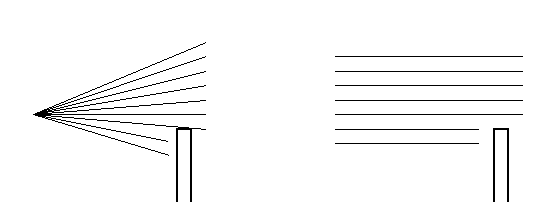
Slika 2.3 Fresnelov i Fraunhoferov ogib
Razlikuju se Fresnelov i Fraunhoferov ogib (Slika 2.3). Zahvaljujuci svojstvima koja pokazuju difraktirani valovi ova pojava nalazi i mnoge primjene u tehnickoj praksi.
Sve ono sto vrijedi za val svjetlosti opcenito, vrijedi i za sve elektromagnetske valove. Medutim, pristup analizi je dvojak, tako da se koristi fizikalna i geometrijska optika, o cemu ce biti vise rijeci kasnije.
 Opcenitiji termin koji
se koristi pri nailasku elektromagnetskog vala na neku povrsinu je rasprsenje (scattering),
Slika 2.4. Pri tom je zraka ABC reflektirana, a ADE difraktirana. Rasprsenje je
posebno izrazito ukoliko su dimenzije objekta na kojeg nailazi elektromagnetski
val reda velicine njegove valne duljine i poglavito ukoliko tih objekata ima
jako mnogo, ili je pak povrsina na koju nailazi val hrapava.
Opcenitiji termin koji
se koristi pri nailasku elektromagnetskog vala na neku povrsinu je rasprsenje (scattering),
Slika 2.4. Pri tom je zraka ABC reflektirana, a ADE difraktirana. Rasprsenje je
posebno izrazito ukoliko su dimenzije objekta na kojeg nailazi elektromagnetski
val reda velicine njegove valne duljine i poglavito ukoliko tih objekata ima
jako mnogo, ili je pak povrsina na koju nailazi val hrapava.
Pri analizi pojave ogiba, a takoder i refleksije, posebno je vazna raspodjela energije oko promatrane zrake vala. U tu se svrhu definiraju Fresnelovi elipsoidi (Slika 2.5) kao prostorni likovi za koje vrijedi (ako se stvar promatra dvodimenzionalno)
![]() (2.1)
(2.1)
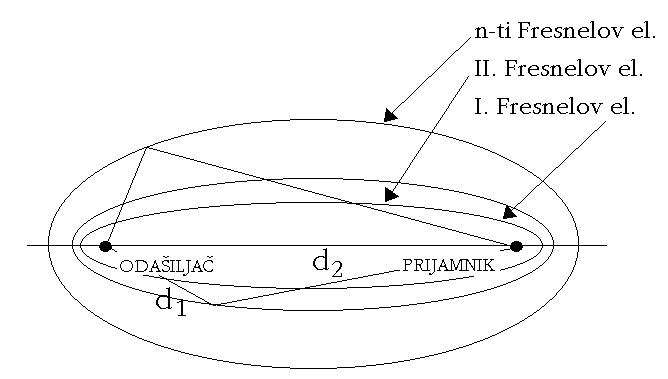
Slika 2.5 Fresnelovi elipsoidi
Ako izvor O zraci sferni val tada valna fronta ima oblik kugline povrsine. Ako izdvojimo dio jedne takove povrsine (ABCD), sve tocke promatrane povrsine imaju jednaku fazu. Prema Huygensovu principu svaka tocka na valnoj fronti je novi izvor sekundarnog vala, te se tako val dalje propagira. Polje na mjestu prijama proporcionalno je povrsini koja zraci, a to je u ovom slucaju cjelokupna povrsina kugle. Sve tocke na promatranoj povrsini su istofazne, ali je njihova udaljenost do tocke prijama P razlicita, tako da je polje na mjestu prijama vektorski zbroj utjecaja razlicito udaljenih istofaznih elementarnih povrsina. Faza se mijenja kontinuirano, ali je moguce izdvojiti povrsine cije zracenje na mjestu prijama stvara istofazni ucinak. Ako udaljenost tocke u kojoj spojnica odasiljaca i prijamnika prolazi kroz promatranu povrsinu ABCD (S) i prijamnika oznacimo sa a, tada ce tocke na povrsini koje su udaljene od prijamnika od (2n-1)l /2 do (2n)l /2 ciniti krivulje koje odreduju povrsine istofaznog ucinka (Slika 2.6).
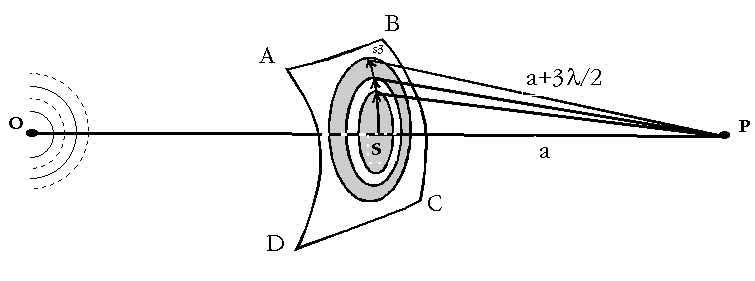
Slika 2.6 Povrsine istofaznog ucinka na mjestu prijama
Ovako dobivene krivulje su ‘kruznice’ kojima je radijus dio luka, i, u stvari, predstavljaju presjeke Fresnelovih elipsoida s dijelom kugline povrsine (na Slici 2.6 izdvojen je slucaj za n=3, pri cemu je luk s3 udaljenost od tocke S do trece krivulje). U realnim se situacijama zbog velikih udaljenosti odasiljaca i prijamnika u odnosu na valnu duljinu moze smatrati da je promatrana povrsina ABCD dio ravnine, dok i dalje treba uzeti u obzir utjecaj pojedinih segmenata te povrsine na fazu signala na prijamnoj strani, radi razlicitih prijedenih putova. Krivulje na ravnini su kruznice radijusa
![]()
![]()
![]() (2.2)
(2.2)
Posto je snaga na mjestu prijama proporcionalna zracecim povrsinama proizlazi da se utjecaj jednog ‘prstena’ ponistava sa dva susjedna ‘poluprstena’
![]()
![]()
![]()
0=0
odnosno
![]()
![]() (2.3)
(2.3)
Ovo znaci da je ukupna snaga polja na mjestu prijama jednaka polovini snage koja bi se dobila da zraci samo povrsina prvog Fresnelovog elipsoida, odnosno glavnina energije elektromagnetskog vala nalazi se u prostoru prvog Fresnelovog elipsoida. Iz toga se izvodi zakljucak da je potrebno analizirati samo one popratne pojave (refleksija, ogib...) koje se dogadaju u volumenu prvog Fresnelovog elipsoida. Stoga se on pojavljuje u svim analizama, a nisu rijetki i slucajevi kada se inzistira da je u propagacijskom modelu prvi Fresnelov elipsoid potpuno ‘prazan’.
Matematicka formulacija Fresnelovih elipsoida
Trodimenzionalni problem se u pravilu promatra dvodimenzionalno pri cemu Fresnelovi elipsoidi postaju elipse. Za elipsu sa ‘sredistem’ u ishodistu (Slika 2.7) vrijedi
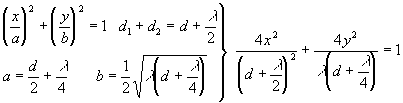

Slika 2.7 Elipsa sa sredistrm u ishodistu
Posto zarista elipse predstavljaju odasiljac i prijamnik zgodnije je promatrati koordinatni sustav s jednim zaristem (odasiljacem) u ishodistu (Slika 2.8).
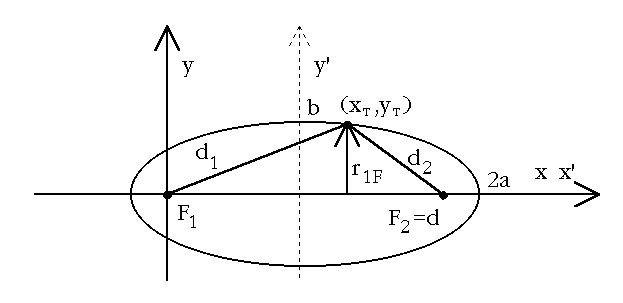
Slika 2.8 Pomaknuta elipsa-Fresnelov ‘elipsoid’
Vrijedi
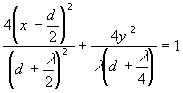
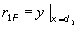
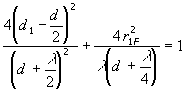
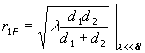 (2.4)
(2.4)
Utjecaj zaobljenosti Zemlje na analizu pojave difrakcije
Zaobljenost Zemljine povrsine ima za posljedicu to da sve tocke, promatrano
u odnosu na spojnicu odasiljac-prijamnik (kako se ocekuje da se se propagirati
elektromagnetski val) imaju vecu visinu (![]() ) od njihove stvarne nadmorske visine (
) od njihove stvarne nadmorske visine (![]() ), Slika 2.9.
), Slika 2.9.
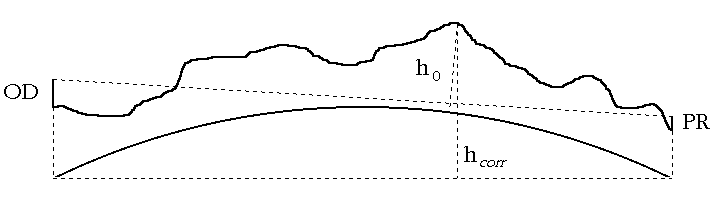
Slika
2.9 Korekcija visina zbog zaobljenosti Zemlje
Pri propagaciji vala prisutna je jos jedna pojava. Naime, zbog loma zrake (refrakcije) koji je posljedica promjenjive gustoce dielektrika u troposferi putanja zrake nije pravocrtna, Slika 2.10.
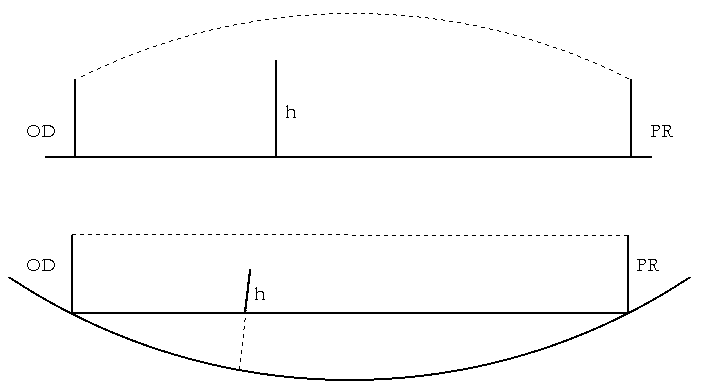
Slika
2.10 Stvarna putanja zrake kroz troposferu i ekvivalentni slucaj
s ravnom putanjom zrake
Stvarna situacija moze se nadomjestiti ekvivalentnom, u kojoj je putanja zrake pravocrtna, ali stvarne nadmorske visine prepreka treba prepraviti. Iznos korekcije ovisi o polozaju izmedu odasiljaca i prijamnika, slicno efektu zaobljenosti Zemljine povrsine, ali suprotno po predznaku. Stoga se cesto ove dvije pojave kombiniraju u jednu, na nacin da se nadmorske visine (h0) nadomjeste stvarnim (hcorr) s obzirom na efektivni radijus Zemlje, koji se uzima uvecan u odnosu na stvarni za odredeni faktor k, sto dovodi do manjih povecanja stvarnih visina. Za standardnu atmosferu vrijedi k=4/3. Moguci su i drugi pristupi ovoj analizi, ali ovakav je uobicajen. Pri svemu ovome vazno je napomenuti da se projekcije visina najcesce uzimaju jednake visinama, jer su zemljopisne velicine takve da su kutevi pri normalizaciji jako mali. O svemu ovome vise moze se naci u lit. [ 7] .
Aproksimacije koje se koriste pri racunanju jakosti polja
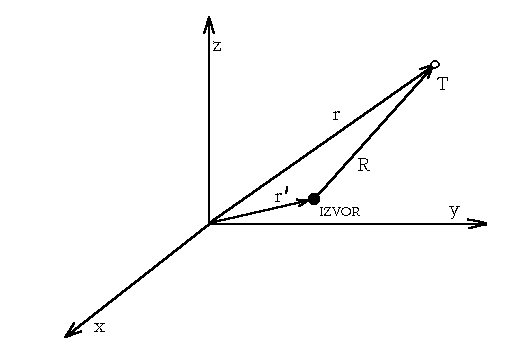
Slika 2.11 Koordinatni sustav i radijus-vektori kod racunanja jakosti polja
Pri izracunu jakosti polja oko nekog izvora, poznate raspodjele naboja, konturnih struja i slicno, uobicajeno je da se cjelokupni prostor raspodijeli u tri preklapajuca podprostora, koji ovise o iznosima radijus vektora R i r u odnosu na valnu duljinu l . Tako u slucaju kada je R reda velicine l nisu moguce nikakve aproksimacije pri racunanju. Ovaj slucaj obicno se naziva blisko polje. Ako je R puno veci od l govori se o dalekom polju koje je karakteristicno za Fraunhoferovu difrakciju. Pri tom se zrake mogu smatrati istofaznima i zanemariti svi clanovi u razvoju u kojima je r potencije 2 ili vise. Izmedu ova dva podrucja je Fresnelovo podrucje u kojem vrijedi isto za clanove R i r, ali je potrebno uzeti u obzir faznu razliku pojedinih zraka.